Entity Transforms #

Overview #

In this page we'll discuss how to convert between different coordinate frames in Minecraft. There are many reasons why you might want to do this:

• If you wanted to build 3D lines using a thin cuboid to visualize some 3d space, you'd need to transform from world coordinates to the entity bones.
• If you wanted to do accurate head-tracking and wanted to measure the angle to a target from a specific joint on your entity.
• If you wanted to fire off a projectile from the tip of a weapon.
• If you wanted to solve IK Chains for limbs to match ground contact points.

Background #

Before we jump into guide, there's a few background topics worth covering.

Matrices #

Generally by the time we send everything to graphics cards we convert things into matrices because it's really efficient to transform many vertices (such as for of a mesh) by a set of matrices. Games often work with other representations, such as quaternions, or in the case of Minecraft Euler rotations, but matrices are good to have a solid understanding of to start with.

If you see a 4x4 matrix full of a bunch of values, if you're not used to working with them, it might seem like you need to have special abilities to see through them, like this.

But, usually the sort of matrices we deal with for 3d transforms are just simply a positional offset and a rotation represented by "Axis vectors" that describe the X, Y, and Z axis, each as a 3-component vector.

When written in a 3x3 matrix the orientation vectors are unit-length vectors (unless there's scale), where these vectors are just like any direction vectors you're used to seeing they have an x,y,z component that define the axis directions of that space.

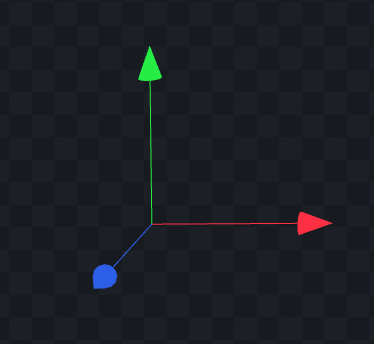
In a 3x3 matrix (especially in textbooks), they're arranged in 2d array along the columns, like this:

[ XAxis.x  YAxis.x  ZAxis.x ]
[ XAxis.y  YAxis.y  ZAxis.y ]
[ XAxis.z  YAxis.z  ZAxis.z ]

In programs you're always going to store the data in memory as <XAxis.x, XAxis.y, XAxis.z, YAxis.x, YAxis.y, YAxis.z, ZAxis.x, ZAxis.y, ZAxis.z>, whether you're row-major or column-major (Wiki about row vs column major), it just means if you're row major you put the XAxis along the row. And if you're math library follows the rules, then it influences the order that things are multiplied together:

With ALL matrix multiplication it's always, row x column.

So, with Row-major to do multiplication of vectors and matrices it's: row_vector * matrix = row_vector:

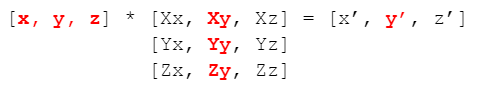
With Column-major to do the same multiplication as the row major, you need to reverse the order:

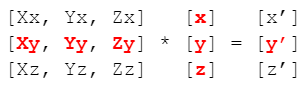
The above distinction is really important to understand, especially if you read some material online to be able to understand the order that data transformed by it will be affected.

So this means, if we have a location relative to our right hand, and we want to know where that is in the world, we first have to transform it by our right hand, then our right elbow, then right shoulder, spine, pelvis, root, entity, etc. all the way until it's in world space. Written in column major that would be:

Entity * RootBone * Pelvis * Spine0 .. SpineN * RShoulder * RightElbow * RightHand * point;

If you get into more complex transforms, it is strongly advised to name your transforms to reflect the space they transform from and to. So for the above we would use something like:

World_To_Entity * Entity_To_Root * Root_To_Pelvis * Pelvis_To_Spine0 .. Spine(N-1)_To_SpineN * SpineN_To_RShoulder * RShoulder_To_RElbow * RElbow_To_RHand * RHand_point;

We'll be less confused about what "space" we're in. The above is described as "local space". Each joint is relative to the parent joint. But if we multiply everything from Root to RHand, the resulting transform is still an RHand transform, it's just in "Character or Entity space". To get it into world space we'd have to multiply World_To_Entity * Entity_To_RHand = World_To_RHand

Technically, this "To" naming is a little confusing because the Entity transform applied to a point really transforms EntityToWorld, but it's applied right to left, so World_To_Entity read right to left is Entity To World. I've also seen: WorldFromEntity * EntityFromRoot. Regardless of "From vs To", what's nice about using this relative rather than absolute naming is that you can also validate your math is right when you see it written:

A_To_B = A_To_Something * Something_To_B
              ^^^^^^^^^^^^^^^^^^^^^

the area denoted: ^ should always match. And combining it removing the middle gives you the natural name of what it does.

Finally, moving on to Minecraft. At the time of this writing, Minecraft doesn't have Transforms you can multiply together, so they aren't inferring a colum or row major notation. You simply get a transform and it's up to you how to apply it. But, having chosen column-major above, we can write down how the operations work as a sequence, and as long as you apply them in order, you'll be ok.

Also, whether we're using a TRS (Transform Rotation Scale combined object), Quaternions, Matrices, or Euler angles, when rotations are involved ORDER DOES MATTER. Rotate A then Rotate B, is not the same as rotate B and then rotate by A.

Get to know the world before we start #

Let's think about those Axis vectors in the unrotated, standard case. We actually can determine which way positive X, Y and Z are, by moving around in the world. When you first spawn into a game for the first time, you're facing due North, as the game calls it. Which if you then walk forward you'll see this increases your Z value. And if you jump you see Y goes up. And that leaves X, which is not right! Well it's not wrong, it's left! As you continue facing North, if you strafe left, this increases your X value. This is a right-handed coordinate system (if you point your fingers towards an axis, and curl them towards the next consecutive axis, your thumb points to the 3rd. XY->Z, YZ->X, wrap for Z: ZX->Y).

Finally!! Let's get started with an Entity #

When creating an entity, I recommend start out in blockbench, and make the first entity you create a simple 3-cardinal axis frame, like so:

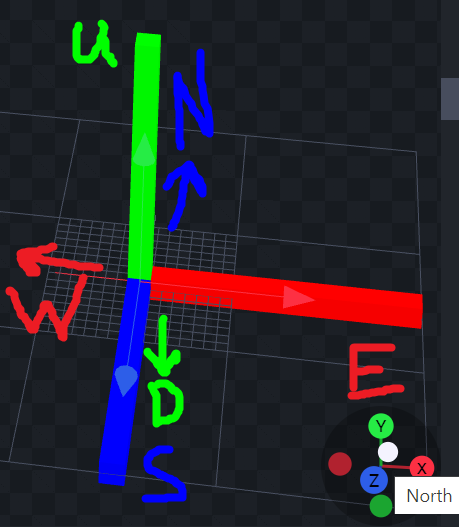
There are several weird things to recognize at this point. Pay very close attention to the directions that Blockbench labels "North, East, South, and West".

1. The first thing to note is that this is rotated 180 degrees from the Minecraft world coordinate system. You should make your Entity face "North" Which is negative Z compared to the game world coordinates.
2. It get's way more strange. If you move boxes in the positive X direction the box coordinates show as positive x values, however if you create a bone, and go to the animation tab, and try adjusting the position of the bone, the move handles are still as expected, but now dragging the handle in the positive direction, actually gives you negative values on X. +X in Animation goes to the west, while +Y still goes up, and +Z still goes south. So in comparison to the Minecraft world, we must flip the Z, and start using a left-handed coordinate frame in the entity.
3. There's a scale factor of 16x in entities. A "Block" or 1 unit in the world, is actually 16 units in entities.

Let's try to group our 3-axis thing under a bone. And then duplicate that group, so we have one we can keep at the entity, and one we can move to a world location.

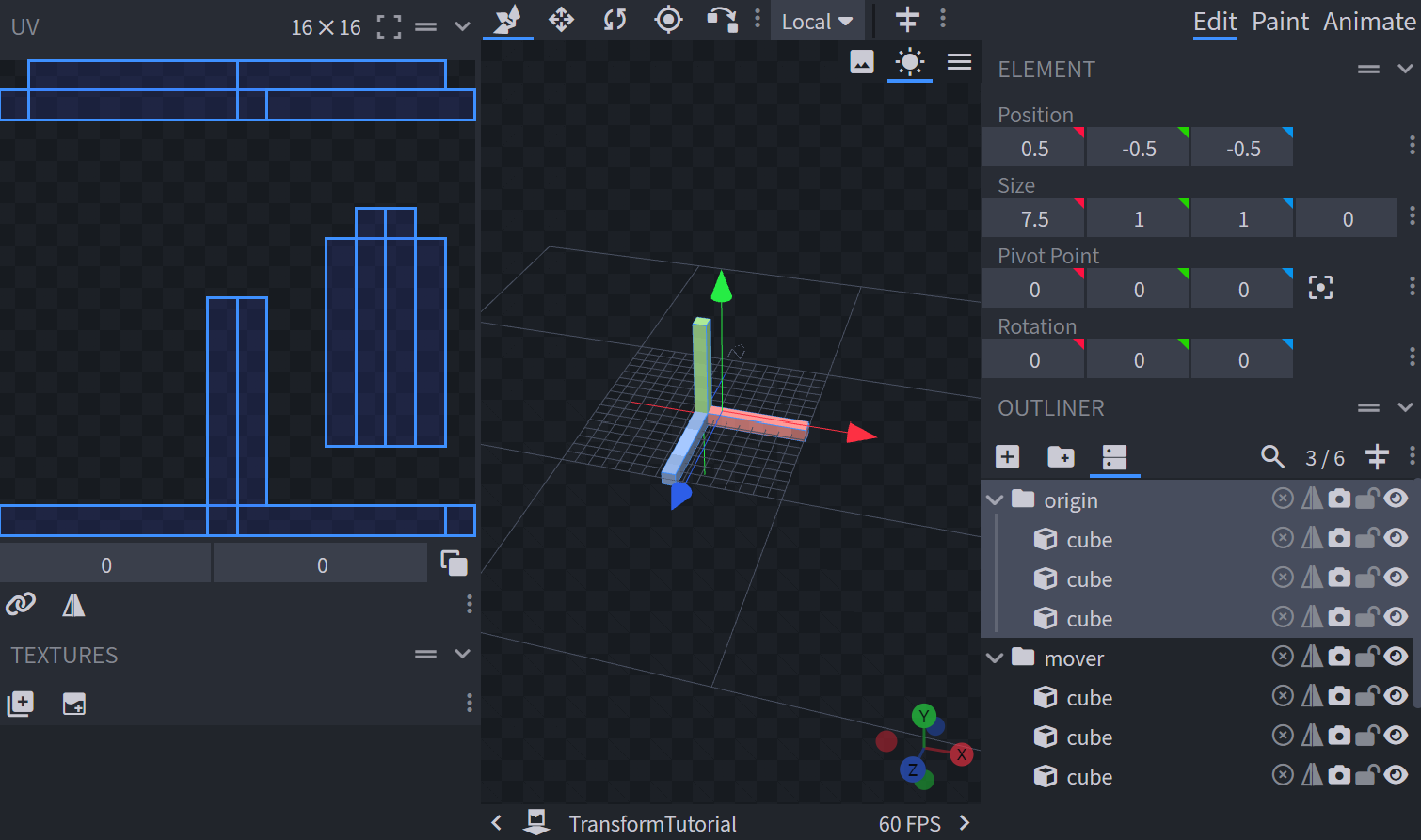
1. Go to the Animate Tab.

2. Create a new Animation.

3. Add a position key for the mover.

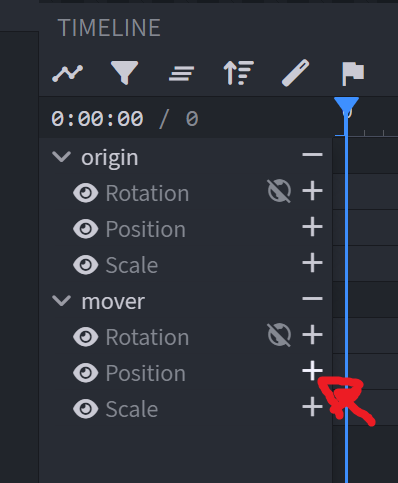
4. Try moving on the X-axis and confirm things are weird.

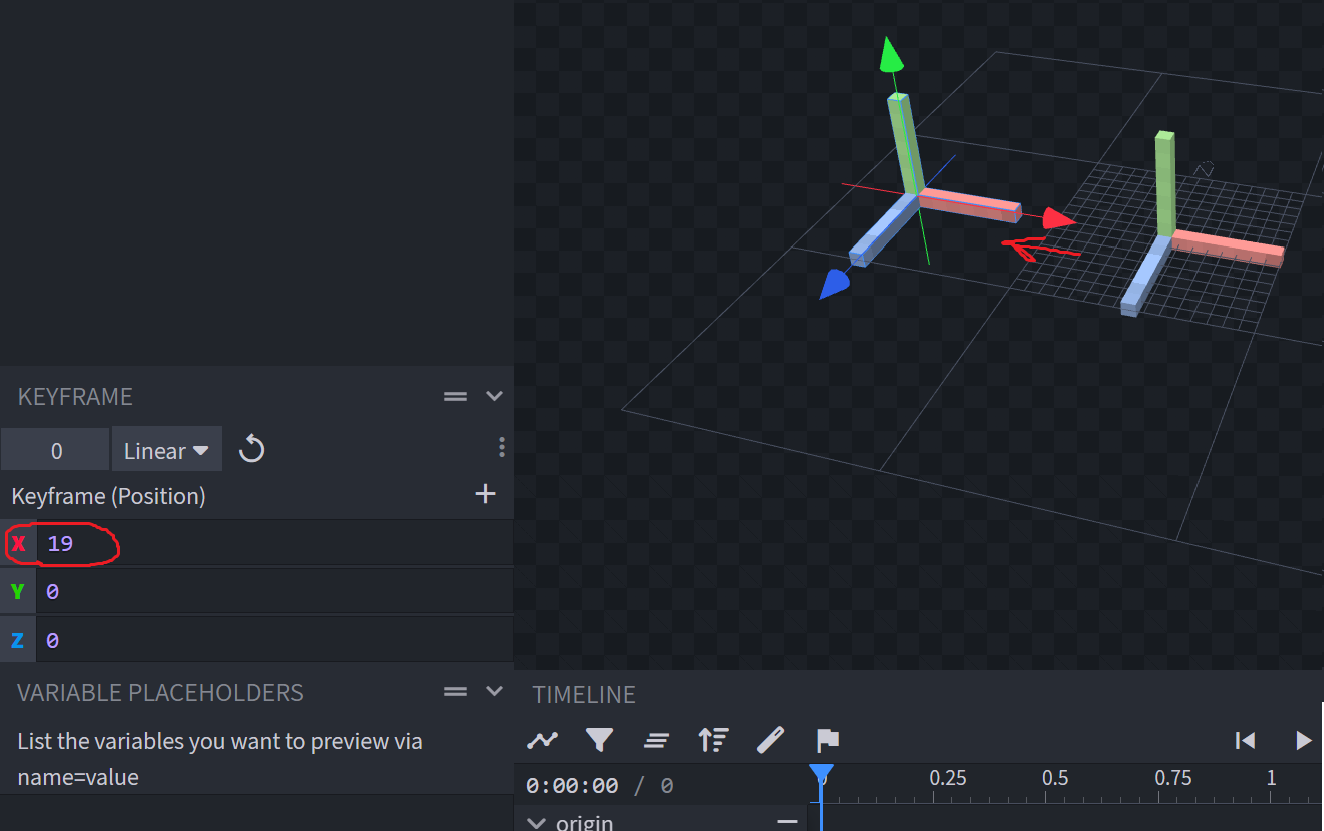
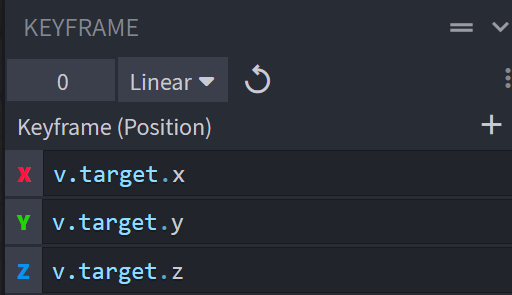
6. Now let's set the position using a variable, we'll set in a pre_animation script.

7. You should be able to mix and match from the minimal robot sample, to get an idea of how to get your entity started. Also you'll save out your blockbench geo, anim. On the behavior side, you don't need much for now. Perhaps just:

"minecraft:physics": {},
"minecraft:collision_box": {},

On the entity side, you just need the minimum to play your animation:

"animations": {
    "myAnim": "animation.tut_transform.move"
},
"scripts": {
    "pre_animation": [
        "// TODO -- we will fill this in next."
    ],
    "animate": [
        "myAnim"
    ]
}

And finally for the script we can do the following:

"
v.target.x = 10;
v.target.y = q.position(1);
v.target.z = 10;

v.target.x = v.target.x - q.position(0);
v.target.y = v.target.y - q.position(1);
v.target.z = v.target.z - q.position(2);

t.cos_yaw = math.cos(q.body_y_rotation);
t.sin_yaw = math.sin(q.body_y_rotation);
t.x = v.target.x;
v.target.x=t.cos_yaw * t.x + t.sin_yaw * v.target.z;
v.target.z=-t.sin_yaw * t.x + t.cos_yaw * v.target.z;

v.target.x = v.target.x * 16;
v.target.y = v.target.y * 16;
v.target.z = -v.target.z * 16;
"

Let's break it down a bit:

pre_animation runs before the animation, and runs this script. The script is intended to be given a position, perhaps your addon will supply the input through parameters from your behavior via a script?

For now you can hard-code these to the world location 10,y,10, where y is just at the same height as the entity.

v.target.x = 10;
v.target.y = q.position(1);
v.target.z = 10;

So in general what we're doing is applying a "TRS" Transform, Rotation, and Scale to get from one space to another.

Technically, remember we would write the transform stack like this:

Translation * RotationZ * RotationY * RotationX * Scale * point;

But, in our case instead of transforming from ent to world, we're going to transform from world to ent. When we have inversable non-commutative math operations like this, the way to apply this inverse is with a property like this:

inverse(A*B) = inverse(B) * inverse(A)

Which means, do the opposite of the operation, in reverse order. So we apply these operations, in this order to our vector.

1. inverse(Translation)
2. inverse(RotationZ)
3. inverse(RotationY)
4. inverse(RotationX)
5. inverse(Scale)

mathematically that looks like:

Inverse(Scale) * Inverse(RotationX) * Inverse(RotationY) * Inverse(RotationZ) * Inverse(Translation) * point;

Which is happening right to left.

1: Inverse(Translation) #

If normally (in forward direction) you're going from ent to world, you'd take your Entity-relative position (like a joint position) and add the entity's. So in reverse, we subtract the entitie's location.

v.target_x = v.target_x - q.position(0);
v.target_y = v.target_y - q.position(1);
v.target_z = v.target_z - q.position(2);

2: Inverse(RotationZ) #

currently entities appear to only be able to adjust from the controllers via pitch and yaw. So no "Z". So we skip that step.

3: Inverse(RotationY) #

To query the entity's yaw, there's a query method: q.body_y_rotation. We'll use that but consider that a positive rotation should make the character turn to the left. Rotating a vector by an angle, is a pretty simple formula, using sin and cos, but getting the sign right is important. Just think if you have a vector that starts facing world +z, and then get's rotated to the left, what will the +X axis become initially positive or initially negative? In our case X left is actually world space still so X left is positive. Likewise, if we had a vector facing positive +X (to the left), and we then started rotating to the left, the Z axis would start becoming?... Yes negative. You only negate the sine term. One last note, t.x is a temporary to save the value of the target

t.cos_yaw = math.cos(q.body_y_rotation);
t.sin_yaw = math.sin(q.body_y_rotation);
t.x = v.target_x;
v.target_x=t.cos_yaw * t.x + t.sin_yaw * v.target_z;
v.target_z=-t.sin_yaw * t.x + t.cos_yaw * v.target_z;

Note, generally, I like to write this as:

new_first_axis = cos(angle) * first_axis - sin(angle) * second_axis;
new_second_axis = sin(angle) * first_axis + cos(angle) * second_axis;

Where first and second axis are the two perpendicular axes to the one being rotated, but in right-hand order. So: XY, YZ, or ZX.

In other words, here's another alternative, that will be more consistent with other Euler angles, XY, and YZ.

t.cos_yaw = math.cos(q.body_y_rotation);
t.sin_yaw = math.sin(q.body_y_rotation);
t.z = v.target.z;
v.target.z=t.cos_yaw * t.z - t.sin_yaw * v.target.x;
v.target.x=t.sin_yaw * t.z + t.cos_yaw * v.target.x;

4: Inverse(RotationX) #

It is legitimately possible I think for entities to pitch, but in practice I haven't seen it. So I just skipped it.

It is an exercise for the reader, though later there will be more info when it comes to bone transforms, so you can get some additional context from that section (when I get to it).

5: Inverse(Scale) #

The last step, is to apply the scale from world to entity. Entities need to be represented with smaller units, so the operation in this direction is multiply. If we were going from ent to world it would be divided by 16.

And there's a sneaky little last negation included here, as was pointed out technically X is flipped from what it SEEMS like it should be in Blockbench when animating, but that actually lines it up with the world coordinate frame, wheres the Z is still opposite. So we just have to flip the Z in the scale step.

v.target.x = v.target.x * 16;
v.target.y = v.target.y * 16;
v.target.z = -v.target.z * 16;